There was a bit of discussion on HN about data representations in dynamic languages, and specifically having values that are either pointers or immediate data, with the two cases being distinguished by use of tag bits in the pointer value:
If there's one takeway/point of interest that I'd recommend looking at, it's the novel way that Ruby shares a pointer value between actual pointers to memory and special "immediate" values that simply occupy the pointer value itself [1].This is usual in Lisp (compilers/implementations) and i wouldn't be surprised if it was invented on the seventies once large (i.e. 36-bit long) registers were available.
I was going to nitpick a bit with the following:
The core claim here is correct; embedding small immediates inside pointers is not a novel technique. It's a good guess that it was first used in Lisp systems. But it can't be the case that its invention is tied into large word sizes, those were in wide use well before Lisp existed. (The early Lisps mostly ran on 36 bit computers.)
It seems more likely that this was tied into the general migration from word-addressing to byte-addressing. Due to alignment constraints, byte-addressed pointers to word-sized objects will always have unused bits around. It's harder to arrange for that with a word-addressed system.
But the latter part of that was speculation, maybe I should try to check the facts first before being tediously pedantic? Good call, since that speculation was wrong. Let's take a tour through some early Lisp implementations, and look at how they represented data in general, and numbers in particular.
Table of Contents
- The problem with integers
- LISP I
- LISP 1.5
- Basic PDP-1 LISP
- M 460 LISP
- PDP-6 LISP
- BBN LISP
- Conclusion
The problem with integers
Before we get started, let's state the problem that tagged pointers solve. In a dynamically typed programming language, the language implementation must be able to distinguish between values of different types. The obvious implementation is boxing; all values are treated as blobs of memory allocated somewhere on the heap, with an envelope containing metadata such as the type and (maybe) the size of the object.
But this means that integers now have tons of overhead. They use up heap space, need to be garbage collected, and new memory needs to be constantly allocated for the results of arithmetic operations. Since integers are so critical to almost all kinds of computing, it would be great to minimize the overhead. And ultimately, to eliminate the overhead completely by encoding small integers as recognizably invalid pointers.
LISP I
I wasn't super hopeful about finding out exactly what numbers looked like in the original Lisp implementation. As far as I know, the source code hasn't been preserved. Now, the original paper describing Lisp ( Recursive Functions of Symbolic Expressions and their Computation by Machine, Part I ) isn't quite as theoretical as the title suggests. For example it describes the memory allocator and garbage collector on a reasonable systems level. But it doesn't mention numbers at all; this is a system for symbolic computation, so numbers might as well not exist.
The LISP I Programmer's Manual from 1960 is more illuminating, though not entirely consistent. In one place the manual claims that LISP I only supports floats, and you'll need to wait until LISP II to use integers. But the rest of the document happily describes the exact memory layout of integers, so who can tell.
A floating point value looks like this:
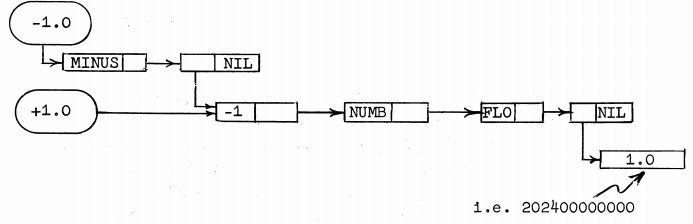
Let's say we have the value 1.0 in a LISP I program. This value is actually pointer to a word. How do we know what the type of the pointed to word is? If the upper half of that word is -1, it's a symbol. Otherwise it's a cons. (The use of -1.0 and 1.0 as the example floats in this picture is unfortunate, since it looks like the -1.0 and -1 are somehow related. That's not the case, -1 is the universal tag value for atoms, and independent of the exact floating point values.)
So the number 1.0 is a symbol? Technically yes, since at this stage of Lisp's
evolution everything is either a symbol or a cons. There are no
other atoms. We can find out if the symbol represents a number by
following the linked list starting from the cdr of
the symbol (a pointer stored in the lower half of the word). If
we find the symbol NUMB on the list, it's some kind
of number. If we find the symbol FLO, it's a floating
point number, and the property list will be pointing to a word
that contains the raw floating point value that this number
represents.
There's a detail here that's kind of amazing. Notice that 1.0 and
-1.0 share the same list structure. The only difference is that
-1.0 has the symbol MINUS in the list, after which
the list merges with the list of 1.0. What a fabulously
inefficient representation! Not only do you have to do a bunch of
pointer chasing just to find the actual value of a number, but
then you'll get to do it again to find out the sign!
The question I can't answer just from reading this document is how exactly the raw floating point value is handled. Surely the garbage collector must know not to interpret those raw bits as pointer data? There is a very detailed example of the memory layout for an integer on pages 94-95, but even with that example I just don't see where the type information is stored. It's clearly not based on address ranges (the raw values are mixed in with the other words), nor the pointer value (all the pointers are stored as 2's complement), nor the 6 unused bits in the machine word.
Suggestions welcome. My best guess is that the example is inaccurate.
LISP 1.5
The LISP 1.5 Programmer's Manual from 1962 explains in a very concise manner how numbers worked in that implementation:
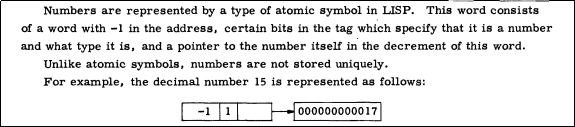
Numbers are still considered to be symbols, and symbols are
still marked with -1 as the car. But the standard
symbol property list is now gone; instead the symbol is pointing
directly to the memory that stores the raw integer value. How
does the program know not to follow that pointer as a list? As the
document says, that's specified by "certain bits in the tag".
The tag? What's the tag? The IBM 704 had a 36-bit word size but just a 15 bit address space. The words were split (on the ISA level) into a 3 bit "prefix", 15 bit "address", 3 bit "tag", and 15 bit "decrement". Since Lisp values are pointers, only the two 15 bit regions are useful for that. One of the 3 bit regions has been repurposed by the Lisp implementation to mark the pointers to raw data.
This is a clear improvement over LISP I, but a number is still represented as an untagged pointer to a tagged pointer to the raw value. Why is the intermediate word there at all, why not go directly with a tagged pointer to the raw value? Maybe code size?
In parallel to that, the address space has now been split into
multiple separate pieces, with the cons cells being allocated from
a different range of addresses than plain data like numbers and
string segments. It could well be that the tagged pointer is
irrelevant to the GC, which just makes its decisions on what's a
pointer based on whether the pointer is contained in the "full
word space" or the "free space". The tags would then be used
just for implementing NUMBERP.
Basic PDP-1 LISP
For a L. Peter Deutsch joint,
The LISP implementation for the PDP-1 Computer
proves to be a surprisingly unsatisfying document. It's almost
exclusively user documentation, with no information on the systems
architecture. Well, except a full source code listing. Guess we'll
have to look at that, then.
NUMBERP is the easiest starting point:
/// ("is a number")
/NUMBERP
nmp, lac i 100
and (jmp
sad (jmp
jmp tru
jmp fal
The main thing that need to be known from the rest of the code is
that the interpreter stores a pointer to the Lisp value that's
currently operated on value at address 100 (octal).
First "lac i 100" follows the pointer to read the
first data words of the value into the accumulator. The next line
looks bizarre; due to the way the PDP-1 macro-assembler
works, "and (jmp" effectively means "and
600000". So this instruction is masking away all but the
top two bits of the accumulator, and "sad
(jmp" is checking whether the result of the masking equals octal
600000. It appears that there is nothing special about the
pointer to a number, but numbers are identified by having the top
two bits set in the pointed-to value.
The next step in understanding the layout is the code for reading the raw value of a number.
/get numeric value
vag, lio i 100
cla
rcl 2s
sas (3
jmp qi3
idx 100
lac i 100
rcl 8s
rcl 8s
jmp x
"lio i 100" loads the current Lisp value into the IO register.
"cla" sets the accumulator to zero. "rcl
2s" then rotates the combination of the IO register and
accumulator by 2 bits. The accumulator now contains as its
low bits the previous high two bits of the IO register. "sas
(3" compares the accumulator to 3; if they're not equal we
jump to qi3 (the error routine for "non-numeric arg for
arith"). "idx 100" moves the pointer to the next word
of the value, and "lac i 100" reads that word into
the accumulator. And finally the combination of the two registers
is rotated by 16 bits, so that we end up with the raw 18 bit value
in the accumulator. Written out step by step the process looks
like this:
. == Bit with value of 0
! == Bit with value of 1
? == Bit with unknown value
0-9, A-H == bits of the integer value
X X+1
------------------------------------------------
[!!23456789ABCDEFGH] [................01]
IO AC
------------------------------------------------
Load IO from address X
[!!23456789ABCDEFGH] [??????????????????]
Clear AC
[!!23456789ABCDEFGH] [..................]
Rotate left by 2
[23456789ABCDEFGH..] [................!!]
Check AC == 3
Load AC from address X+1
[23456789ABCDEFGH..] [................01]
Rotate left by 8
[ABCDEFGH..........] [........0123456789]
Rotate left by 8
[..................] [0123456789ABCDEFGH]
Clearly an integer is now represented by a pointer to two words that has a special tag in the high bits of the first word. This implementation got rid of the extra layer of indirection in LISP 1.5; an integer is now just a pointer to tagged data. But we're still left with the storage of a one-word integer requiring three words.
Why use a layout that requires shuffling data around this much, instead of just having the tag in X and the raw value in X+1? It seems awfully inconvenient. My best guess is that the top 1-2 bits of the second word are reserved for the GC, e.g. for use as mark bits. But understanding exactly how the GC works is maybe a project for another day.
M 460 LISP
Before starting research for this article, I'd never heard of the early Lisp implementation for the Univac M 460. A description of the system can be found in the 1964 collection The programming language LISP: Its operation and applications .
Numbers and print names are placed in free storage using the device that sufficiently small (i.e., less than 2^10) half-word quantities appear to point into the bit table area and so don't cause the garbage collector any trouble. A number is stored as a list of words (a flag-word and from 1 to 3 number words, as required), each number word containing in its CAR part 10 significant bits and sign. Thus an integer whose absolute value is less than 2^11 will occupy the same amount of storage (2 words) as in 7090 LISP 1.5.
This is another bit of progress! The key insight on the road to tagged pointers is that invalid parts of the address space can be used to distinguish between pointers and immediate data. Another important insight in this paper is that most numbers in a program are going to be small, so it might make sense to have variable representations for numbers of different magnitude. But it's not a full realization of the concept yet, immediate small numbers are not accessible directly by the user. They are internal to the implementation, used as a building block for boxed integers of various levels of inefficiency.
The paper gets even better once we get a few more pages in, since for characters M 460 Lisp does take that final step:
Each character in the character set available on the M 460 (including tab, carriage return, and others) is represented internally by an 8-bit code (6 bits for the character (up to case), 1 bit for case, and 1 bit for color). To facilitate the manipulation of character strings within our LISP system, we permit such character literals to appear in list structure as if they were atoms, i.e. pointers to property lists. These literals can, where necessary, be distinguished from atoms since they are less than 2^8 in magnitude and hence, viewed as pointers, don't point into free storage (where, as in 7090 LISP, property lists are stored). The predicate charp simply makes this magnitude test.
That's about as clear a case of using embedding immediate data in pointers as it gets. It's just that the tag is rather large (22 highest bits, rather than the 1-4 lowest bits you'd expect today). And it's also dealing with characters rather than numbers, so let's carry on with the investigation a bit longer.
PDP-6 LISP
The June 1966 report on PDP-6 LISP has the following to say on integers:
Fixed-point numbers >= 0 and < about 4000 are represented by a "pointer" 1 greater than their value, and no additional list structure. All other numbers use a pointer to full-word space as part of an atom header with a FIXNUM or FLONUM indicator.
This is starting to get close to the modern fixnum, except for no facility for immediate negative numbers and a tiny range. (This is a machine with 36 bit words and 18 bit pointers; one would hope for a bit more than 12 bits for immediate integers).
BBN LISP
Structure of a LISP system using two-level storage is a wonderful systems design paper from November 1966, describing BBN LISP for a PDP-1 with 16K of core memory, 88K of absurdly slow drum memory, and no hardware paging support. How do you make efficient use of the drum memory? By some clever data layout, software-driven paging, and a locality-optimizing memory allocator.
So it's actually a paper I thought was totally worth reading just for its own sake. But for the purposes of this post, this is the money quote:
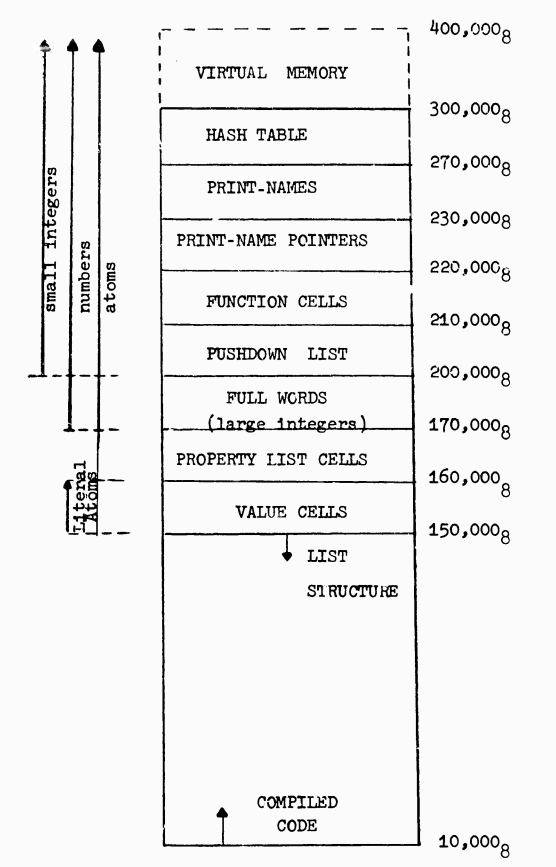
LISP assumes that it is operating in an environment containing 128K words, that is from 0 to 400,000 octal. Only 88K actually exist on the drum. The remaining portion of the address space is used for representation of small integers between -32,767 and 32,767 (offset by 300,000 octal), as described below.
The paper describes a machine with both an 18-bit word size and address space, with 16-bit signed fixnums embedded in the pointers. That's about as good as it gets. (Though not quite optimal; they're using bit 17 as the integer tag, but what happened to bit 18? The paper doesn't say, but odds are that it's again a GC mark bit).
The particularly observant reader might have noticed that this machine had 104K words of physical memory, but the described tagging scheme only leaves 64K words addressable. What's up with that? On one level it's exactly what M 460 LISP and PDP-6 Lisp were doing: that 40K of address space stores things that can't be directly pointed to from another Lisp value. But those other implementations were just opportunistically reusing the parts of address space that contained native code.
By contrast, BBN LISP carefully arranged for there to exist as much of such storage as possible, and for it to be located above the address 200,000 (octal).
The most clever example of that is the representation of symbols. The first implementations we saw just implemented symbols as a list of properties indexed by name (e.g. name, value cell, function cell, etc). An obvious optimization is to allocate a symbol as a single larger block of memory with fixed slots for the most common properties, and a generic property list slot to contain anything else.
What BBN Lisp does instead is allocate a symbol in multiple separate blocks rather than a single contiguous one. A pointer to the symbol will point to the block of value cells, so reading the value cell is trivial. What if you want to read another property, e.g. the function? We look at the offset of the value cell pointer to the start of the value cell block, and access the function cell block at the same offset. In modern parlance it ends up as an structure-of-arrays layout rather than an array-of-structures.
In addition to getting more address space for fixnums, they also got exactly the same kind of locality improvements that an structure-of-arrays would be used for today. So it was an all-around neat optimization.
There is also an early design document for BBN 940 LISP from almost the same time as the above paper. It appears to describe the kind of elaborate tagging scheme that a modern Lisp might use, and places the tags in the low bits where they're easier to test for/eliminate. And they even call heap-allocated numbers "boxed"! I had no idea this terminology was in use 50 years ago. The relevant section:
There will be a maximum of 16 pointer types of objects in the 940 LISP System. These are (numbered in octal)
- 00. S-expressions (nonatomic)
- 01. Identifiers (literal atoms)
- 02. Small Integers
- 03. Boxed Large Integers
- 04. Boxed Floating Point Numbers
- 05. Compiled Function - Lambda Type
- 06. Compiled Function - Lambda Type - Indef Args
- 07. Compiled Function - Mu Type - Args Paired
- 10. Compiled Function - Mu Type - List of Args
- 11. Compiled Function - Macro
- 12. Array - Pointers
- 13. Array - Integers
- 14. Array - FP #s
- 15. Strings - Packed Character Arrays
- 16.
- 17. Pushdown List Pointers
Each pointer will be contained in one 940 word of 24 bits. Bits 0 and 1 will be nominally empty, and may in some cases be used by the system (e.g. bit 0 for garbage collection) or perhaps even the user (in S-expressions). The four bits 2-5 will contain the type number for this pointer. The 18 bits 6-23 will contain an effective address (in the LISP drum file) where the referenced information is stored.
It looks like they ended up not using this design for BBN 940 LISP, and it instead uses an extended version of the segmented memory scheme from the PDP-1 implementation described earlier in this section. But even if these particular bits weren't practical to use with that hardware, at this point just about all the ideas for tagged pointers have definitely been invented.
Conclusion
The initial LISP I implementation in 1960 had the least efficient implementation of numbers this side of church numerals, where even just getting the value might imply chasing half a dozen pointers. But new implementations optimized that layout aggressively. By 1964, the M 460 LISP implementation had arrived at the general solution of using pointers to invalid parts of the address space for storing immediate data, but user-accessible integers were still boxed; the only use for the unboxed integers was as an internal building block. In 1966 PDP-6 LISP applied the idea of tagged immediate data to tiny positive integers, and the PDP-1 based BBN LISP took the idea to the logical conclusion, and allowed immediate storage of integers of almost the full machine word.
I would not have guessed that these optimizations were discovered and applied so early and so aggressively. It's also noteworthy that this was independent of both the machine word size, address space size, and addressing mode of the machine. The first fully fledged implementation I found was on a machine with 18 bit words, 18 bits of address space, and word-addressing. That should have been just about the worst case!
There's an interesting tangent with how MacLISP ended up reversing this progress in the '70s and going back to boxed integers, since they wanted to have just a single integer representation. I won't go into the details since this post already grew longer than intended. But for those interested in the subject AI Memo 421 is a fun read.
Was the technique definitely first used in Lisp? These implementations are early enough that there aren't a ton of other possibilities. The only ones I can think of would be APL and Dartmouth BASIC. If anyone can find documentation on earlier uses of storing immediate data in tagged pointers, please let me know and I'll edit the article.
There is an interesting encoding maybe used on 64 bit machines.
By setting up the virtual address space it is possible to ensure that all values are either a valid 64 ieee floating point value that points to an unmapped address if treated as a pointer or a NaN value that is a valid address.