So there I was, implementing a one element ring buffer. Which, I'm sure you'll agree, is a perfectly reasonable data structure.

It was just surprisingly annoying to write, due to reasons we'll get to in a bit. After giving it a bit of thought, I realized I'd always been writing ring buffers "wrong", and there was a better way.

Array + two indices

There are two common ways of implementing a queue with a ring buffer.

One is to use an array as the backing storage plus two indices to the array; read and write. To shift a value from the head of the queue, index into the array by the read index, and then increment the read index. To push a value to the back, index into the array by the write index, store the value in that offset, and then increment the write index.

Both indices will always be in the range 0..(capacity - 1). This is done by masking the value after an index gets incremented.

That implementation looks basically like: 

uint32 read;
uint32 write;
mask(val)  { return val & (array.capacity - 1); }
inc(index) { return mask(index + 1); }
push(val)  { assert(!full()); array[write] = val; write = inc(write); }
shift()    { assert(!empty()); ret = array[read]; read = inc(read); return ret; }
empty()    { return read == write; }
full()     { return inc(write) == read; }
size()     { return mask(write - read); }

The downside of this representation is that you always waste one element in the array. If the array is 4 elements, the queue can hold at most 3. Why? Well, an empty buffer will have a read pointer that's equal to the write pointer; a buffer with capacity N and size N would also have have a read pointer equal to the write pointer. Like this:

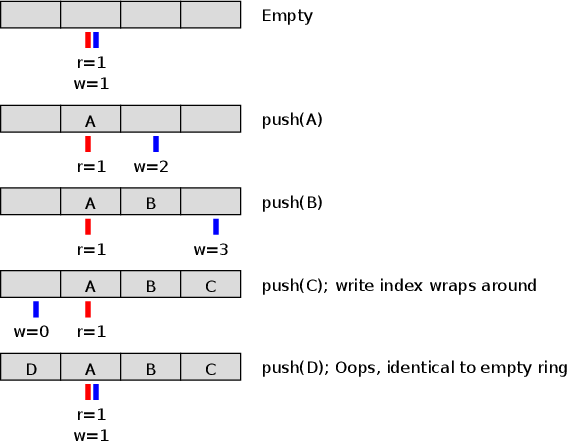
The 0 and 4 element cases are indistinguishable, so we need to prevent one from ever happening. Since empty queues are kind of necessary, it follows that the latter case needs to go. The queue has to be defined as full when one element in the array is still unused. And that's the way I've always done it.

Losing one element isn't a huge deal when the ring buffer has thousands of elements. But when the array is supposed to have just one element... That's 100% overhead, 0% payload!

Array + index + length

The alternative is to use one index field and one length field. Shifting an element indexes to the array by the read index, increments the read index, and then decrements the length. Pushing an element writes to the slot that "length" elements after the read index, and then increments the length. That looks something like this: 

uint32 read;
uint32 length;
mask(val)  { return val & (array.capacity - 1); }
inc(index) { return mask(index + 1); }
push(val)  { assert(!full()); array[mask(read + length++)] = val; }
shift()    { assert(!empty()); --length; ret = array[read]; read = inc(read); return ret; }
empty()    { return length == 0; }
full()     { return length == array.capacity; }
size()     { return length; }

This uses the full capacity of the array, with the code not getting much more complex.

But at least I've never liked this representation. The most common use for ring buffers is for it to be the intermediary between a concurrent reader and writer (be it two threads, to processes sharing memory, or a software process communicating with hardware). And for that, the index + size representation is kind of miserable. Both the reader and the writer will be writing to the length field, which is bad for caching. The read index and the length will also need to always be read and updated atomically, which would be awkward.

(Obviously my one element ring buffer wasn't going to be used in a concurrent setting. But it's a matter of principle.)

Array + two unmasked indices

So is there an option that gets the benefits of both representations, without introducing a third state variable? (Whether it's two indices + a size, or two indices + some kind of a full vs. empty flag). Turns out there is, and it's really simple. It uses two indices, but with one tweak compared to the first solution: don't squash the indices into the correct range when they are incremented, but only when they are used to index into the array. Instead you let them grow unbounded, and eventually wrap around to zero once the unsigned integer overflows. So:

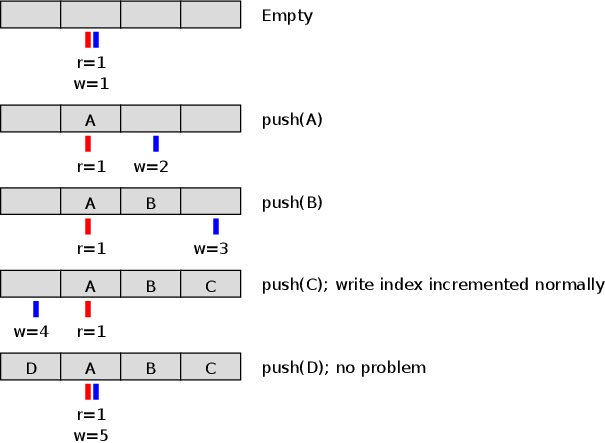
This reclaims the wasted slot. The code modifying the indices also becomes simpler, since the clumsy ordering of increments vs. array accesses was only needed for maintaining the invariant that the index is always in range. 

uint32 read;
uint32 write;
mask(val)  { return val & (array.capacity - 1); }
push(val)  { assert(!full()); array[mask(write++)] = val; }
shift()    { assert(!empty()); return array[mask(read++)]; }

Checking the status of the ring also gets simpler: 

empty()    { return read == write; }
full()     { return size() == array.capacity }
size()     { return write - read; }

This all works, assuming the following restrictions:

  • The implementation language supports wraparound on unsigned integer overflow. If it doesn't, this approach doesn't really buy anything. (What will happen in these languages is that the indices get promoted to bignums which will be bad, or they get promoted to doubles which will be worse. So you'll need to manually restrict their range anyway).
  • The capacity must always be a power of two. (Edit: This limitation does not come just from the definition of mask using a bitwise and. It applies even if mask were defined using modular arithmetic or a conditional. It's required for the code to be correct on unsigned integer overflow.)
  • The maximum capacity can only be half the range of the index data types. (So 2^31-1 when using 32 bit unsigned integers). In a way that could be interpreted as stealing the top bit of the index to function as a flag. But the case against flags isn't so much the extra memory as having to maintain the extra state.

All of those seem like non-issues. What kind of a monster would make a non-power of two ring anyway?

This is of course not a new invention. The earliest instance I could find with a bit of searching was from 2004, with Andrew Morton mentioning in it a code review so casually that it seems to have been a well established trick. But the vast majority of implementations I looked at do not do this.

So here's the question: Why do people use the version that's inferior and more complicated? I've must have written a dozen ring buffers over the years, and before being forced to really think about it, I'd always just used the first definition. I can understand why a textbook wouldn't take advantage of unsigned integer wraparound. But it seems like it should be exactly the kind of cleverness that hackers would relish using and passing on.

  • Could it just be tradition? It seems likely that this is the kind of thing one learns by osmosis, and then never revisits. But even so, you'd expect the "good" implementations to push out the "bad" ones at some point, which doesn't seem to be happening in this case.
  • Is it resistance to having code actually take advantage of integer overflow, rather than it be a sign of a bug?
  • Are non-power of two capacities for ring buffers actually common?

Join me next week for the exciting sequel to this post, "I've been tying my shoelaces wrong all these years".